Rangkuman Lengkap Beserta Klarifikasi Bahan Limit Fungsi (Limit Searah Dan Aturan Limit)
pada June 24, 2017
Limit Fungsi
Limit suatu fungsi menggambarkan apa yang terjadi dengan nilai-nilai fungsi f, yaitu f(x), apabila x mendekati suatu nilai a tertentu.
Misalkan fungsi f didefinisikan sebagai f(x) = x + 2. Jika x mendekati 1 maka nilai-nilai f(x) sanggup dilihat pada tabel berikut:
x mendekati 1 dari arah kiri | x mendekati 1 dari arah kanan | |||||||||
x | 0,8 | 0,9 | 0,95 | 0,99 | 0,999 | 1 | 1,001 | 1,01 | 1,05 | 1,1 |
f(x) | 2,8 | 2,9 | 2,95 | 2,99 | 2,999 | 3 | 3,001 | 3,01 | 3,05 | 3,1 |
Dari tabel di atas terlihat bahwa x mendekati 1, tetapi x kurang dari 1 (x mendekati 1 dari arah kiri), maka nilai f(x) mendekati 3. Demikian pula bila x mendekati 1, tetapi x lebih besar dari 1 (x mendekati 1 dari arah kanan), maka f(x) juga mendekati 3. Hal menyerupai ini sanggup dikatakan sebagai berikut:
1. "Jika x mendekati 1, tetapi x tidak sama dengan 1 maka nilai f(x) mendekati 3" atau
2. "Limit dari f(x) kalau x mendekati 1 yaitu 3"
Pernyataan menyerupai di atas biasanya dituliskan dengan lebih ringkas sebagai berikut:
Misalkan fungsi f terdefinisikan pada selang terbuka I yang memuat a, kecuali mungkin di a. Limit f(x) dikala x mendekati a sama dengan L, ditulis
apabila nilai f(x) sanggup dibentuk sedekat mungkin ke L, dengan cara mengambil nilai x yang cukup bersahabat ke a, tetapi x # a.
Catatan
1. Notasi lain untuk limit f(x) dikala x mendekati a sama dengan L yaitu f(x) --> L, bila x -->a
2. Fungsi f tidak harus terdefinisi di a
3. Jika f terdefinisi di a, f(a) tidak harus sama dengan L
Contoh Soal 2:
Misalkan fungsi f didefinisikan sebagai berikut:
maka f(x) = x + 2, kalau x # 1
Perhatikan bahwa:
1. f(1) tidak terdefinisikan.
2. Jika x mendekati 1, tetapi x # 1, maka dari tabel di atas terlihat pula bahwa f(x) mendekati 3.
3. =3 "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
Contoh berikut ini menunjukkan bahwa limit fungsi mungkin tidak ada.
Contoh Soal 3
Misalkan fungsi f didefinisikan sebagai f(x) = 1/x , x # 0. Perhatikan nilai-nilai f(x) kalau x mendekati 0 pada tabel berikut:
x < 0 | f(x) | x > 0 | f(x) |
-2 | -1/2 | 2 | ½ |
-1 | -1 | 1 | 1 |
-1/2 | -2 | 1/2 | 2 |
-1/4 | -4 | 1/4 | 4 |
-0,1 | -10 | 0,1 | 10 |
-0,01 | -100 | 0,01 | 100 |
-0,001 | -1000 | 0,001 | 1000 |
-0,0001 | -10000 | 0,0001 | 10000 |
Dari tabel diatas sanggup dilihat bahwa:
1. Jika x mendekati 0 dari arah kiri, maka f(x) semakin membesar negatif (dengan kata lain mengecil)
2. Bila x mendekati 0 dari arah kanan, maka f(x) semakin membesar positif.
3. Tidak sanggup ditentukan suatu nilai tertentu yang dituju oleh f(x).
4. Dikatakan bahwa  "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
tidak ada.
Dari contoh-contoh di atas sanggup dilihat bahwa:
1. Limit suatu fungsi pada suatu bilangan tidak selalu sama dengan nilai fungsi pada bilangan tersebut.
2. Mungkin saja terjadi bahwa ada sedangkan f(c) tidak terdefinisi.
Dengan kata lain, kalau kita ingin memilih limit f(x) kalau x mendekati c, maka tidak perlu dipermasalahkan apakah f(c) ada atau tidak ada.
Kasus-kasus Limit yang Sama
Kasus 1 | Kasus 2 | Kasus 3 |
f(a) = L | f(a) # L | f(a) tidak diketahui |
ketiga masalah di atas ini menawarkan limit yang sama yaitu =L "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
Limit Searah
Misalkan fungsi f terdefinisi pada selang [a,b), kecuali mungkin di a. Limit kanan f(x) dikala x mendekati a (atau limit f(x) dikala x mendekati a dari sisi kanan) sama dengan L, sanggup dituliskan sebagai berikut:
apabila nilai f(x) sanggup dibentuk sedekat mungkin ke L, dengan cara mengambil nilai x yang cukup bersahabat ke a dan x > a.
Misalkan fungsi f terdefinisi pada selang (b,a], kecuali mungkin di a. Limit kiri f(x) dikala x mendekati a (atau limit f(x) dikala x mendekati a dari sisi kiri) sama dengan L, sanggup dituliskan sebagai berikut:
apabila nilai f(x) sanggup dibentuk sedekat mungkin ke L, dengan cara mengambil nilai x yang cukup bersahabat ke a dan x < a.
Hubungan limit disuatu titik dengan limit satu sisi
Contoh Soal 4
Diketahui fungsi f yang didefinisikan sebagai =\sqrt{x},x\geq&space;0 "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
. Tentukan  "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
bila ada.
Pembahasan
Fungsi akar kuadrat terdefinisi untuk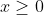 
, sehingga =0 "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
tetapi  "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
tidak ada. Dengan demikian tidak ada.
Hukum Limit
Pada bab aturan limit ini akan dibahas mengenai sifat-sifat limit yang sanggup dipakai untuk menghitung limit suatu fungsi, yang disebut Hukum Limit.
Misalkan c yaitu konstanta, n yaitu bilangan bundar positif dan kedua limit  "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
dan  "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
ada, maka
1. 
2. 
3. )=c\lim_{x\rightarrow&space;a}f(x) "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
4. +g(x))=\lim_{x\rightarrow&space;a}f(x)+\lim_{x\rightarrow&space;a}g(x) "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
5. -g(x))=\lim_{x\rightarrow&space;a}f(x)-\lim_{x\rightarrow&space;a}g(x) "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
6. .g(x))=\lim_{x\rightarrow&space;a}f(x).\lim_{x\rightarrow&space;a}g(x) "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
7. }{g(x)}=\frac{\lim_{x\rightarrow&space;a}f(x)}{\lim_{x\rightarrow&space;a}g(x)} "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
8. 
9. )^{n}=(\lim_{x\rightarrow&space;a}f(x))^{n} "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
10. 
11. }={\sqrt[n]{\lim_{x\rightarrow&space;a}f(x)}} "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
CATATAN:
Jika ATAU tidak ada maka kesebelas rumus di atas tidak berlaku.
Contoh Soal 5
Dengan memakai sifat-sifat limit, tentukan limit berikut ini:
1.  "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
2. 
Pembahasan
1. Dengan aturan limit nomor ke-4, ke-2 dan kemudian aturan limit ke-1 diperoleh:
= 7 x 3 + 1 ......(Hukum limit ke-1)
= 22
2. Dengan memperhatikan aturan limit ke-7 maka, sanggup dituliskan sebagai berikut:
Perhitungan diatas sanggup dilanjutkan apabila penyebutnya tidak sama dengan nol . Karena pada soal sebelumnya telah diketahui bahwa penyebutnya tidak sama dengan nol, maka sanggup dilanjutkan lagi menyerupai berikut ini:
Jika diperhatikan dua pola diatas merupakan fungsi polinom dan fungsi yang rasional. Dengan aturan limit sanggup ditunjukan bahwa substitusi pribadi selalu berlaku untuk fungsi yang demikian.
Hal itu menyerupai pernyataan berikut ini:
Jika f yaitu fungsi polinom atau fungsi rasional dan a dalam kawasan asal f maka:
Contoh Soal 6
Hitunglah pada fungsi-fungsi f berikut ini:
(1) f(x) = 12, untuk a = 5
(2) f(x) = -2x -5, untuk a = -1
(3) =4-3x+2x^{2}-x^{3} "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
, untuk a = 2
Pembahasan
(1) 
..........(Perhatikan aturan limit ke-1)
(2) Pengerjaannya serupa menyerupai pola soal sebelumnya.
= -2(-1) - 5
= -3
(3) =\lim_{x\rightarrow&space;2}4-\lim_{x\rightarrow&space;2}3x+\lim_{x\rightarrow&space;2}2x^{2}-\lim_{x\rightarrow&space;2}x^{3} "Rangkuman Lengkap Beserta Penjelasan Materi Limit Fungsi (Limit Searah dan Hukum Limit)")
= -2