Cara Memilih Garis Singgung Antara Dua Lingkaran

Garis Singgung Dua Lingkaran.Sobat pernah lihat mesin giling ataupun roda sepeda? Bila teman lihat lagi di sepeda terdapat rantai yang menghubungkan antara gear roda dengan gear pedal. Nah dua roda gear itulah yang disebut dua bulat dan rantai itu desebut garis singgungnya. Lebih tepatnya garis singggung komplotan luar. Kaprikornus sanggup diartikan bahwa garis singgung bulat yakni garis yang sempurna menyinggung dua lingkaran.

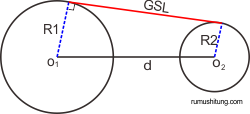
1. Garis Singgung Persekutuan Luar

Panjang Garis Singgung Persekutuan Luar Lingkaran

– Lingkaran besar dengan sentra O1 dan jari-jari R1
– Lingkaran kecil dengan sentra O2 dan jari-jari R2
– d = jarak antara dua titik sentra bulat (antara O1 dan O2)
– GSL = Garis Singgung Persekutuan Luar Lingkaran.
Dari mana sih asal rumus tersebut? Coba teman amati gambar berikut,

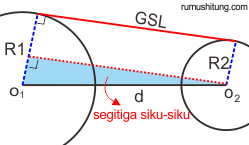
Rumus mencari garis singgung dua bulat (garis persekutuan) sebetulnya berasal dari hukum phytagoras, Lihat segitiga siku-siku berwarna biru. Dengan segitiga itu kita sanggup menghitung panjang garis GSL dengan pythagoras d(O1-O2) dan Selisih jari-jari bulat besar (R2) dengan jari-jari bulat kecil. maka didapatlah persamaan rumus garis singgung dua bulat menyerupai ini

R1-R2 = seisih jari-jari.
Lalu bolehkah dibalik menjadi R1-R2?

Boleh alasannya yakni pada prinsipnya bilangan negatif dan kasatmata kuadratnya akan selalu positif. Sobat harus hati-hati dengan tanda negatif (-) dan Positif (+).

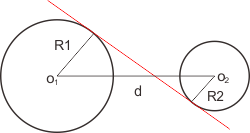
2. Garis Singgung Persekutuan Dalam

Panjang Garis Singgung Persekutuan Luar Lingkaran =

Dari mana asal rumus tersebut? Sama menyerupai pada garis singgung bulat luar, ini hanya hukum phytagoras. Lihat gambar di bawah ini

Lihat segitiga yang berwarna kuning. Kelihatan kan dari mana asal rumusnya. Yap, dari pythagoras antara d (jarak antar sentra lingkaran) dengan jumlah R1 dan R2. So didapatlah rumus menyerupai yang diatas. Buat teman hitung, ini ada cara menghafalnya..

DALAM = TAMBAH (sama-sama ada M)

Tweet