Penjelasan Menganai Penyelesaian Spl Dengan Metode Eliminasi Gauss

Ada beberapa metode yang sanggup dipakai untuk memilih penyelesaian Sistem Persamaan Linear (SPL) AX = B. Kali ini akan dibahas hanya satu metode saja, yaitu Metode Eliminasi Gauss.

Metode ini memakai Operasi Baris Dasar (OBD) yang telah dibahas pada postingan sebelumnya.

Ringkasan dibawah ini akan menawarkan bahwa Sistem Persamaan Linear (SPL) gres yang diperoleh dengan Operasi Baris Dasar (OBD) memiliki penyelesaian yang sama dengan Sistem Persamaan Linear (SPL) sebelumnya.

Now, coba perhatikan SPL yang diberikan berikut ini:

$\begin{matrix} 3x_{1} &- &x_{2} &= &1 \\ x_{1} &+ &x_{2} &= & 3 \end{matrix}\Leftrightarrow \begin{pmatrix} 3 &-1 \\ 1 &-1 \end{pmatrix}\begin{pmatrix} x_{1}\\ x_{2} \end{pmatrix}=\begin{pmatrix} 1\\ 3 \end{pmatrix}$

yang memiliki penyelesaian $x_{1}=1$ dan $x_{2}=2$ .

Matriks gandeng dari SPL tersebut di atas adalah:

$\begin{pmatrix} 3 &-1| &1 \\ 1 & 1| &3 \end{pmatrix}$

Dengan memperhatikan SPL tersebut:

Jika baris pertama dan baris kedua dari matriks gandeng tersebut dipertukarkan tempatnya maka akan diperoleh matriks gandeng berikut:

$\begin{pmatrix} 3 &-1| &3 \\ 1 & 1| &1 \end{pmatrix}$

Jika matriks gandeng yang telah ditukar tersebut dikembalikan dalam bentuk SPL, yaitu:

$\begin{matrix} 3x_{1} &- &x_{2} &= &3 \\ x_{1} &+ &x_{2} &= & 1 \end{matrix}$

dan lalu diselesaikan, maka akan diperoleh penyelesaian $(x_{1},x_{2})=(1,2)$ yang sama dengan penyelesaian SPL sebelumnya.

Misalkan baris kedua matriks gandeng (yang belum di tukar) di atas dikalikan dengan 5 maka akan diperoleh matriks gandeng berikut:

$\begin{pmatrix} 15 &-5 &| & 5\\ 1 &1 & | & 3 \end{pmatrix}$

Jika SPL ini pun diselesaikan maka akan diperoleh penyelesaian $(x_{1},x_{2})=(1,2)$ dimana hasil SPL tersebut sama dengan hasil SPL sebelumnya (awal).

Jika baris pertama matrik gandeng dikalikan dengan minus satu (-1) lalu ditambahkan ke baris kedua, maka akan diperoleh matriks gandeng sebagai berikut:

$\begin{pmatrix} 3 &-1 &| & 1\\ -2 &2 & | & 2 \end{pmatrix}$

Jika SPL ini diselesaikan maka akan diperoleh penyelesaian yang sama, yaitu pasangan bilangan $(x_{1},x_{2})=(1,2)$ .

Terlihat bahwa suatu SPL memiliki penyelesaian yang sama dengan SPL asal jikalau dikenai operasi-operasi:

1. Menukarkan persamaan ke-i dengan persamaan ke-j

2. Mengalihkan persamaan ke-i dengan konstanta tak k

3. Menambahkan persamaan ke-i dengan k kali persamaan ke-j

Prinsip dari metode eliminasi Gauss ialah diperolehnya SPL gres yang memiliki penyelesaian yang sama dengan SPL sebelumnya, tetapi SPL gres tersebut lebih gampang diselesaikan.

Perhatikan referensi di bawah ini:

Tentukan penyelesaian SPL berikut ini:

$\begin{matrix} x_{1} & + &2x_{2} &+ &x_{3} & = &3 \\ 3x_{1} & - & x_{2} &- & 3x_{3} & = &-1 \\ 2x_{1} &+ &3x_{2} &+ &x_{3} &= & 4 \end{matrix}$

Jawaban:

Perhatikan matriks gandeng SPL tersebut:

$\begin{pmatrix} 1 &2 &1 & | &3 \\ 3 &-1 & -3 & | &-1 \\ 2 &3 &1 &| & 4 \end{pmatrix}$

Dengan melaksanakan Operasi Baris Dasar akan diperoleh matrik gandeng :

$\begin{pmatrix} 1 &2 &1 & | &3 \\ 0 &-7 & -6 & | &-10 \\ 0&-1 &-1 &| & -2 \end{pmatrix}$

Pada langkah ini, $a_{11}=1$ dipakai untuk mengeliminasi (membuat nol) unsur-unsur di bawahnya.

Sekarang, sanggup dilakukan OBD yang menghasilkan matriks gandeng sebagai berikut:

$\begin{pmatrix} 1 &2 &1 & | &3 \\ 0 &-7 & -6 & | &-10 \\ 0&0 &-1/7 &| & -4/7 \end{pmatrix}$

dari matriks gandeng tersebut sanggup diketahui bahwa p(A) = p(A|B) yang berarti SPL tersebut konsisten. Sehingga matriks tersebut sanggup dituliskan sebagai berikut:

$\begin{matrix} x_{1}&+ &2x_{2} &- &x_{3} &= &3 & & &(1) \\ & &-7 x_{2} &+ &6x_{3} &= &-10 & & &(2) \\ & & & & -1/7x_{3} &= &-4/7 & & & (3) \end{matrix}$

Dari persamaan (3) diperoleh 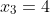$x_{3}=4$ . Kemudian nilai 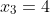$x_{3}=4$ ini disubstitusikan ke dalam persamaan (2) sehingga diperoleh $x_{2}=-2$ . Selanjutnya, kedua nilai tersebut disubstitusikan ke dalam persamaan (1) maka akan diperoleh $x_{1}=3$ . Cara substitusi yang ibarat ini dikenal sebagai substitusi mundur. Jadi, penyelesaian SPL tersebut ialah $\mathbf{X}=(x_{1},x_{2},x_{3})^{T}=(3,-2,4)^{T}$ .

Prosedur pengeliminasian unsur-unsur SPL (untuk n = 4) sanggup diberikan dalam sketsa di bawah ini:

$\begin{pmatrix} \mathbf{P} &x &x &x &| &x \\ x &x &x &x &| &x \\ x &x &x &x &| &x \\ x &x &x &x &| &x \end{pmatrix}\rightarrow \begin{pmatrix} x &x &x &x &| &x \\ 0 &\mathbf{P} &x &x &| &x \\ 0 &x &x &x &| &x \\ 0 &x &x &x &| &x \end{pmatrix}$

$\rightarrow \begin{pmatrix} x &x &x &x &| &x \\ 0 &x &x &x &| &x \\ 0 &0 &\mathbf{P} &x &| &x \\ 0 &0 &x &x &| &x \end{pmatrix}\rightarrow \begin{pmatrix} x &x &x &x &| &x \\ 0 &x &x &x &| &x \\ 0 &0 &x &x &| &x \\ 0 &0 &0 &x &| &x \end{pmatrix}$

Setelah diperoleh matriks ibarat ini, maka periksa kekonsistenan SPL. Jika ya, maka lakukan substitusi mundur untuk memilih penyelesaiannya.

Contoh

Tentukan penyelesaian dari SPL berikut ini:

$\begin{matrix} 2x_{1} &- &x_{2} &+ &x_{3} &= &2\\ x_{1} &+ &2x_{2} &+ &x_{3} &= &1\\ 4x_{1} &+ &3x_{2} &+ &3x_{3} &= &4\\ 3x_{1} &+ &x_{2} &+ &2x_{3} &= &3 \end{matrix}$

Jawab:

$\begin{pmatrix} 2 &-1 &1 \\ 1 &2 &1 \\ 4 &3 &3 \\ 3 &1 &2 \end{pmatrix}\begin{pmatrix} x_{1}\\ x_{2}\\ x_{3} \end{pmatrix}=\begin{pmatrix} 2\\ 1\\ 4\\ 3 \end{pmatrix}$

Jika dilakukan OBD terhadap matriks gandengnya maka akan diperoleh:

$\begin{pmatrix} 1 &2 &1 &|&1 \\ 0 &-5 &-1 &| &0\\ 0 &0 &0 &| &0\\ 0 &0 &0 &|&0 \end{pmatrix}$

Terlihat bahwa p(A) = p(A|B), sehingga SPL tersebut konsisten. Dari matriks terakhir diperoleh:

$\begin{matrix} x_{1} &+ &2x_{2} &+ &x_{3} &= &1 & & &(1) \\ & &-5x_{2} &- &x_{3} &= &0 & & & (2) \end{matrix}$

Sehingga terdapat 2 persamaan dan 3 variabel yang harus ditentukan nilainya. Ini berarti terdapat 1 variabel yang nilainya bebas/sembarang. Misalkan $x_{2}=k$ , dengan k merupakan bilangan real sembarang. Maka dari persamaan (2) diperoleh $x_{3}=-5k$ ,kemudian substitusikan kedua nilai tersebut sehingga akan diperoleh bahwa $x_{1}=1+3k$ .

Makara penyelesaian dari SPL ini ialah $\mathbf{X}=(x_{1},x_{2},x_{3})^{T}=(1+3k,k,-5k)^{T}$ , dengan k ialah suatu konstanta. Perhatikan bahwa SPL ini memiliki banyak penyelesaian (karena p(A) = 2 < 3).

Penjelasan Menganai Penyelesaian Spl Dengan Metode Eliminasi Gauss

No comments