Rangkuman Bahan Peluang Matematika

Pada permodelan stokastik kita sering perlu menilik validitas suatu model dengan memakai data empirik.

Agar sanggup memperoleh data empirik yang menggambarkan sikap suatu fenomena, kadangkala kita perlu mengadakan percobaan yang sanggup diulang dalam kondisi yang sama.

Meskipun diulang dalam kondisi yang sama, hasil percobaan ini tidak sanggup ditebak dengan tepat, namun kita mengetahui semua kemungkinan hasilnya.

Ruang Contoh
Himpunan semua hasil suatu percobaan acak disebut ruang pola atau yang sering disebut ruang sampel. Lambangnya dinotasikan dengan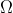 (omega).

Setiap unsur atau anggota ruang pola disebut titik contoh.

Ruang pola suatu percobaan akan berbeda-beda tergantung dari tujuan percobaan tersebut atau tergantung dari apa yang diamati terhadap hasil suatu percobaan.

Kejadian
Kejadian yakni himpunan bab suatu ruang contoh.

Kita katakan suatu kejadian E,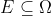 , muncul atau terjadi kalau hasil percobaan berpadanan dengan sebuah unsur dari E.

Suatu kejadian yang hanya terdiri atas satu unsur ruang pola disebut kejadian sederhana.

Kejadian-kejadian lainnya, intinya sanggup dinyatakan sebagai adonan dari beberapa kejadian sederhana dan disebut dengan kejadian majemuk.

Komplemen Suatu Kejadian
Jika E yakni suatu kejadian, maka pelengkap (tandingan) dari E yang biasa ditulis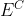 . Komplemen suatu kejadian yakni suatu kejadian yang unsurnya yakni semua anggota ruang pola 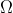yang tidak merupakan unsur dari E.

Dua Kejadian Lepas
Jika E dan F yakni dua kejadian, maka E dan F disebut dua kejadia lepas atau terpisah, kalau dan hanya kalau tidak ada unsur dari E yang juga merupakan unsur dari F atau sebaliknya.

Gabungan Dua Kejadian
Gabungan dua kejadian E dan F, ditulis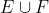 yakni suatu kejadian yang unsurnya yakni semua unsur ruang pola yang termasuk unsur kejadian E atau unsur kejadian F atau unsur keduaya (E dan F).

Irisan Dua Kejadian
Irisan dua kejadian E dan F yang dituliskan sebagai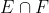 yakni suatu kejadian yang unsurnya yakni semua unsur ruang pola yang sekaligus termasuk unsur kejadian E dan kejadian F.

Medan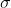 (sigma)
Medan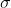 (sigma) yakni suatu himpunan f  yang anggotanya yakni himpunan bab dari ruang pola serta memenuhi syarat-syarat di bawah ini:
1.
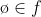
2. Ji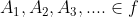ka maka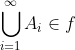
3. Ji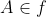ka maka 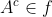dengan 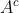menyatakan pelengkap dari A.

Jadi, suatu himpunan f disebut medan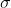 (sigma) kalau 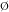yakni anggota dari f, f  tertutup terhadap operasi adonan takhingga, dan f tertutup terhadap operasi komplemen.

Misalkan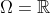 dan f yakni himpunan semua selang terbuka di R. Jika 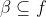sehingga B  yakni suatu medan 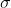, maka B disebut medan Borel, dan anggotanya disebut himpunan Borel.

Aksioma Peluang
Suatu ukuran peluang P pada yakni suatu fungsi P : f ---> [0,1] yang memenuhi syarat-syarat berikut ini :
1. Untuk setiap kejadian A berlaku
2.
3. Jika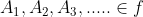 yakni barisan kejadian-kejadian yang saling lepas yaitu 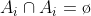untuk setiap pasangan i,j dengan i # j, maka:


Pasangan disebut dengan ruang peluang.

Aksioma peluang diatas merupakan aturan-aturan yang harus dipatuhi biar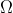 dan P memenuhi syarat sebagai suatu model peluang.

Misalkan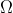 yakni ruang pola suatu percobaan, serta E dan F yakni dua kejadian. Kita sebut E dan F mempunyai kemungkinan yang sama untuk terjadi kalau P(E) = P(F).

Berikut ini merupakan jawaban dari aksioma perluang di atas: 
PERTAMA. Peluang dari himpunan kosong yakni 0, . Peluang dari himpunan kosong disebut juga dengan kejadian mustahil.

KEDUA. Jika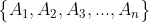 yakni himpunan kejadian-kejadian lepas, maka:


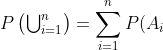KETIGA. Jika ruang pola terdiri atas N titik pola yang masing-masing berpeluang sama untuk terjadi, serta kejadian A terdiri atas N(A) unsur, maka:
P(A) = N(A) / N

KEEMPAT. Untuk sembarang kejadian E, maka:


KELIMA. Jika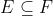 maka:


KEENAM. Jika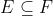 maka P(E) 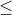P(F)

KETUJUH.

KEDELAPAN.

Tweet