Rangkuman, Pola Soal Dan Pembahasan Dari Integral Taktentu Dan Integral Tentu

Matematika mempunyai banyak pasangan operasi balikan: penambahan dan pengurangan, perkalian dan pembagian, serta pemangkatan dan penarikan akar. Dalam setiap kasus, operasi kedua"menghapuskan" operasi yang pertama, dan sebaliknya. Salah satu keuntungannya yaitu kegunaannya dalam menuntaskan suatu persamaan. Misalnya untuk memecahkan mmmm, kita melaksanakan penarikan akar. Sebelumnya niscaya kita telah mengetahui turunan suatu fungsi. Jika kita bermaksud menuntaskan persamaan yang melibatkan turunan, maka kita memerlukan operasi balikannya, yaitu antiturunan atau integrasi.

Dengan turunan dan antiturunan kita sanggup menuntaskan banyak problem antara lain: penentuan ketinggian pesawat ulang-aling pada waktu tertentu, penentuan kosumsi energi di Jakarta pada suatu hari, peramalan jumlah populasi (penduduk, bakteri, dll.) dimasa yang akan datang, dan lain sebagainya. Kaprikornus misalkan diberi turunan suatu fungsi, bagaimana caranya mencari fungsi yang memenuhinya??

Integral Taktentu

(Antiturunan) Fungsi F disebut antiturunan dari f pada selang I jikalau F'(x) = f(x) untuk setiap x anggota di I.

Ilustrasi:

$f(x)=x^{3}\Rightarrow F(x)=\frac{1}{4}x^{4}$

$f(x)=x^{3}\Rightarrow F(x)=\frac{1}{4}x^{4}+5$

$f(x)=\cos x\Rightarrow F(x)=\sin x$

$f(x)=\cos x\Rightarrow F(x)=\sin x+C$

Contoh Soal 1:

Tunjukan bahwa $F(x)=\frac{1}{3}x^{3}+5x+2$ merupakan antiturunan dari fungsi $f(x)=x^{2}+5$

Pembahasan:

F merupakam antiturunan dari fungsi f jikalau F'(x) = f(x). Perhatikan, karena

$F'(x)=x^{2}+5=f(x)$

maka F merupakan antiturunan dari f.

Suatu fungsi sanggup mempunyai lebih dari satu antiturunan. Dari pola soal di atas, $G(x)=\frac{1}{3}x^{3}+5x+20$ atau $H(x)=\frac{1}{3}x^{3}+5x-25$ juga merupakan antiturunan dari f.

Jika F antiturunan dari f pada selang I, maka antiturunan dari f yang paling umum adalaj F(x) + C, dengan C merupakan konstanta sembarang.

Contoh Soal 2:

Periksa dengan pendiferensialan bahwa rumus berikut benar:

1. $\int \frac{x}{\sqrt{x^{2}+1}}dx=\sqrt{x^{2}+1}+C$

2. $\int x\cos x dx=x\sin x+\cos x+C$

Pembahasan:

1. Karena

$\frac{\mathrm{d} }{\mathrm{d} x}\begin{pmatrix} \sqrt{x^{2}+1}+C \end{pmatrix}=\frac{1}{2}(x^{2}+1^{-1/2})(2x)$

$=\frac{2x}{2(x^{2}+1)^{1/2}}$

$=\frac{x}{(x^{2}+1)^{1/2}}$

Sehingga sanggup dituliskan sebagai berikut:

$\int \frac{x}{\sqrt{x^{2}+1}}dx=\sqrt{x^{2}+1}+C$

maka investigasi kita telah terbukti.

2. Karena

$\frac{\mathrm{d} }{\mathrm{d} x}(x\sin x+\cos x+C)=\sin x+x\cos x-\sin x$

$=x\cos x$

Sehingga sanggup dituliskan sebagai berikut:

$\int x\cos xdx=x\sin x+\cos x+C$

maka investigasi kita telah terbukti.

Beberapa antiturunan fungsi yang sering dipakai diberikan sebagai berikut: ( Dengan k, C yaitu konstanta dan F'(x) = f(x), G(x)' = g(x) )

No Fungsi Antiturunan

1 k f(x) kF(c) + C

2 $f(x)\pm g(x)$ $F(x)\pm G(x)$

3 $x^{n},n\neq -1$ $\frac{x^{n+1}}{n+1}+C$

4 sin x - cos x + C

5 cos x sin x + C

6 $\sec ^{2}x$ tan x + C

7 $\csc ^{2}x$ - cot x + C

8 sec x tan x sec x + C

9 csc x cot x - csc x + C

Lambang Antiturunan

Pada turunan kita biasanya memakai lambang $D_{x}$ untuk turunan suatu fungsi terhadap x. Dengan semangat yang sama, lambang antiturunan terhadap x dituliskan sebagai $A_{x}$ . Jadi, jikalau F antiturunan f maka sanggup ditulis sebagai:

$A_{x}f(x)=F(x)+C$

Selain memakai notasi di atas, notasi yang lebih sering atau umum yaitu dengan memakai notasi Leibniz yang selanjutnya dikenal sebagai integral taktentu, yaitu jikalau F anti turunan f maka sanggup dituliskan sebagai berikut:

$\int f(x)dx=F(x)+C$

(Integral Taktentu) Misalkan F yaitu antiturunan f. Integral taktentu f(x) terhadap x adalah
$\int f(x)dx=F(x)+C$

Catatan:

1. Hasil integral tak tentu berupa suatu fungsi, sedangkan hasil integral tentu berupa suatu bilangan.

2. Integral taktentu yaitu lambang lain dari antiturunan

Contoh Soal 3:

Tentukan:

$\int (x^{2}+2x+\frac{2}{x}+\sin x+e^{x}+2)dx$

Pembahasan:

$\int (x^{2}+2x+\frac{2}{x}+\sin x+e^{x}+2)dx=\frac{1}{3}x^{3}+x^{2}+2\ln |x|-\cos x+e^{x}+2x+C$

Contoh Soal 4:

Tentukan:

$\int (1-t)(2+t^{2})dt$

Pembahasan:

$\int (1-t)(2+t^{2})dt=\int (2+t^{2}-2t-t^{3})dt$

$=2t+\frac{1}{3}t^{3}-t^{2}-\frac{1}{4}t^{4}+C$

Contoh Soal 5:

Tentukan:

$\int (x^{2}+2x+1)\begin{pmatrix} \frac{1}{x} \end{pmatrix}dx$

Pembahasan:

$\int (x^{2}+2x+1)\begin{pmatrix} \frac{1}{x} \end{pmatrix}dx=\int \begin{pmatrix} x+2+\frac{1}{x} \end{pmatrix}dx$

$=\frac{1}{2}x^{2}+2x+\ln |x|+C$

Contoh Soal 6:

Tentukan:

$\int \begin{pmatrix} \frac{3-x^{2}+2\sqrt{x}}{x^{2}} \end{pmatrix}dx$

Pembahasan:

$\int \begin{pmatrix} \frac{3-x^{2}+2\sqrt{x}}{x^{2}} \end{pmatrix}dx=\int \frac{3}{x^{2}}dx-\int \frac{x^{2}}{x^{2}}dx+\int \frac{2\sqrt{x}}{x^{2}}dx$

$=\int 3x^{-2}dx-\int 1dx+\int 2x^{-3/2}dx$

$=-3x^{-1}-x+2(-2)x^{-1/2}+C$

$=\frac{-3}{x}-x-4x^{-1/2}+C$

Integral Tentu

Jika suatu integral dihitung pada interval tentu, maka integral tersebut diberi batas pengintegralan dan dinamakan Integral Tentu. Aturan perhitungan integral tentu dan sifat-sifat integral yaitu sebagai berikut:

(Teorema Dasar Kalkulus) Misalkan F'(x) = f(x) maka
$\int_{a}^{b}f(x)dx=F(b)-F(a)$

Berdasarkan Teorema Dasar Kalkulus, untuk mengevaluasi integral tentu f pada selang [a,b] dilakukan dengan cara sebagai berikut:

1. Tentukan antiturunan dari fungsi f, yaitu F

2. Evaluasi/hitung F(b) - F(a)

Contoh Soal 7:

Hitunglah

$\int_{-1}^{2}(4x-6x^{2})dx$

Pembahasan:

$\int_{-1}^{2}(4x-6x^{2})dx=4\int_{-1}^{2}xdx-6\int_{-1}^{2}x^{2}dx$

$=4\begin{pmatrix} \frac{4}{2}-\frac{1}{2} \end{pmatrix}-6\begin{pmatrix} \frac{8}{3}+\frac{1}{3} \end{pmatrix}$

= -12

Sifat-sifat Integral Tentu

1. $\int_{b}^{a}f(x)dx=-\int_{a}^{b}f(x)dx;b> a$

2. $\int_{a}^{a}f(x)dx=0$

3. $\int_{a}^{b}cdx=c(b-a)$

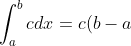4. $\int_{a}^{b}cf(x)=c\int_{a}^{b}f(x)dx; c konstanta$

5. $\int_{a}^{b}[f(x)\pm g(x)]dx=\int_{a}^{b}f(x)dx\pm \int_{a}^{b}g(x)dx$

6. $\int_{a}^{b}f(x)dx+ \int_{b}^{c}f(x)dx=\int_{a}^{c}f(x)dx$

Contoh Soal 8:

Diketahui $\int_{0}^{2}f(x)dx=4$ dan $\int_{2}^{0}(g(x)-f(x))dx=5$ . Gunakan sifat-sifat integral untuk menghitung:

a. $\int_{2}^{0}(2f(x)-3)dx$

b. $\int_{0}^{2}g(x)dx$

Pembahasan:

a. Untuk bab pertama diperoleh sebagai berikut:

$\int_{2}^{0}(2f(x)-3)dx=-\int_{0}^{2}(2f(x)-3)dx$

$=-\int_{0}^{2}2f(x)dx+\int_{0}^{2}3dx$

$=-2\int_{0}^{2}f(x)dx+3(2-0)$

= -2 x 4 + 6

= -2

b. Untuk bab kedua diperoleh sebagai berikut:

Diketahui $\int_{2}^{0}(g(x)-f(x))dx=5$ maka:

$\int_{0}^{2}(g(x)-f(x))dx=-5$

$\int_{0}^{2}g(x)dx-\int_{0}^{2}f(x)dx=-5$

$\int_{0}^{2}g(x)dx=-5+\int_{0}^{2}f(x)dx$

= -5 + 4

= -1